強誘電体の原子変位と強く結合した歪みに関連する全エネルギー表面の第一原理計算による自動的な評価方法
研究の背景
チタン酸バリウムBaTiO3やチタン酸鉛PbTiO3のペロブスカイト型酸化物ABO3は工業的応用上非常に重要な強誘電体である.
これらの物質が示す大きな誘電率や圧電特性からBaTiO3ベースの物質が固体コンデンサーなど,
PbTiO3ベースの物質は圧電素子や振動センサーなどに応用されている.
BaTiO3,PbTiO3ともキュリー温度 (それぞれ 383 K,763 K)
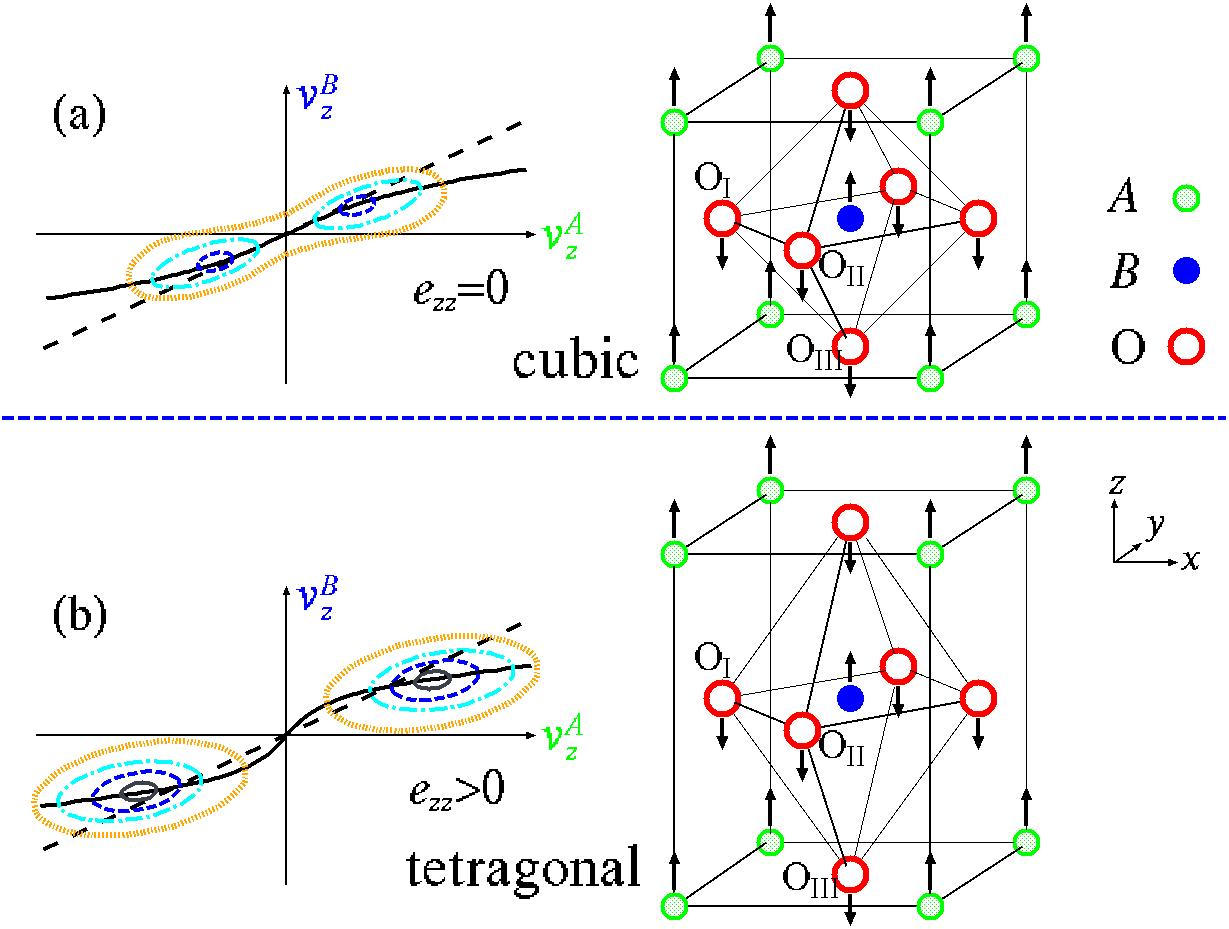
以上では単位胞の体積もほぼ等しく約64Å3の立方晶(Oh1,図1(b))を呈するが,
温度降下にともない構造相転移を起こし,室温付近ではC4v1の対称性をもつ正方晶(図1(d)で原子変位がある場合)が安定構造である.
自発分極はこのABの陽イオンと3つのO陰イオンが構造相転移に伴って逆方向に変位する結果であり,
大きな圧電効果はこの原子変位と格子の歪みが強く結合 (coupling)
しているためと考えることが出来る.
なお,BaTiO3とPbTiO3とは結晶構造と単位胞の体積以外はかなり異なった性質を示す.
たとえば正方晶の格子定数の比 c/a は室温でそれぞれ1.01,1.06であるし,
BaTiO3ではB=Tiイオンの原子変位ほうがA=Baのそれより大きいのに対し、
PbTiO3では逆にA=Pbの原子変位ほうがB=Tiのそれより大きい.
BaTiO3はさらに低温で斜方晶,三方晶に構造相転移をするが,PbTiO3は正方晶を保つ.
図1にペロブスカイト型酸化物強誘電体ABO3の原子変位とゾーン中心歪みの結合の様子,
すなわち原子変位で張られた空間の中の全エネルギー表面を示す.
z方向への歪ezzが0から大きくなるに従って原子変位の安定位置は原点から遠くに移動し深くなり,
最安定構造を超えると浅くなってゆく.逆に原子変位ゼロに対応する原点のエネルギーは高くなりより不安定になる.
第一原理計算によってこの全エネルギー面を正確に把握することは
キュリー温度や物性の温度変化などのペロブスカイト型酸化物強誘電体の物性を予測する上で極めて重要である.
1994年,
King-SmithとVanderbiltは擬ポテンシャル法によりこの全エネルギー面の評価を行った
[R. D. King-Smith and David Vanderbilt: Phys. Rev. B 49, 5828 (1994), doi:10.1103/PhysRevB.49.5828].
しかしながら,彼らは歪みがゼロの時のΓ15ソフトモード固有ベクトルξの方向(図1中の破線)
に沿った原子変位についてでのみ,その変位の大きさの4次関数で全エネルギを評価したため,
次の3つの欠点があった.
- 立方晶→正方晶に歪む際のエネルギーゲインを誤って評価する.
- 全エネルギーを原子変位の大きさuの関数としてみた場合,正方晶の平衡構造よりさらに歪んだ領域で実際の関数から外れる.
- uの4次の項は歪みにも強く依存するため4次の項の決定が困難である.
正確な全エネルギー表面の自動的な評価方法
そこで西松は上記3つの問題を解決するため,完全立方構造からの原子変位vατと「変位の大きさ」uαの関係を
uα2 = (vαA)2+(vαB)2+(vαOI)2+(vαOII)2+(vαOIII)2 と定義し直し,
u=sqrt(ux2+uy2+uz2)一定条件下で{vατ}と{eαβ}とについて構造最適化計算を行うことにより,
全エネルギー表面をuの関数として得るという,
より正確な全エネルギー面の自動的な評価方法,すなわち,図1に実線で示した谷底線を自動的に辿る方法を開発した
[Takatoshi Hashimoto, Takeshi Nishimatsu et al.: Jpn. J. Appl. Phys. 43, 6785 (2004), doi:10.1143/JJAP.43.6785].
具体的にはラグランジュの未定乗数法を巧妙に用いた構造最適化方法である.
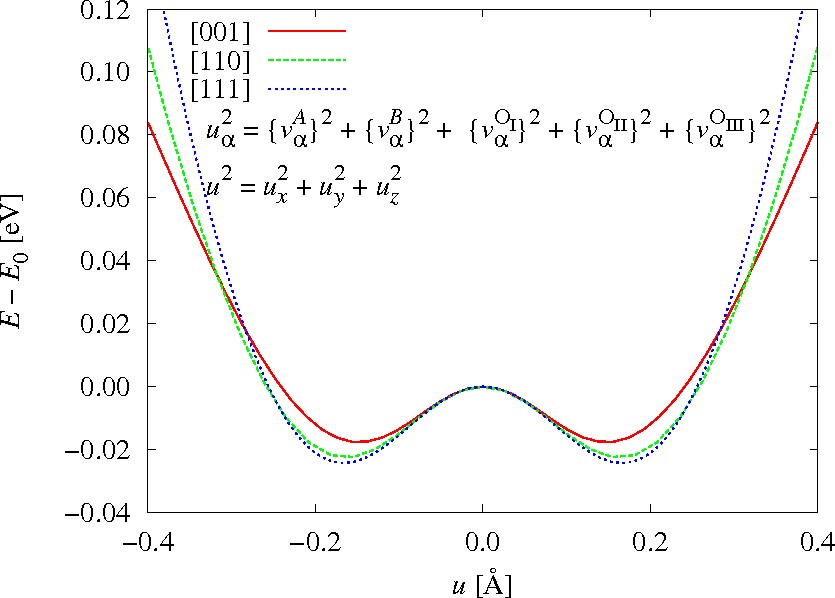
BaTiO3に適用し,全エネルギをuの関数としてプロットしたものを図2に示す.
本最適化方法のKing-SmithとVanderbiltの手順と比べたときの利点をまとめると
- 新しく開発した構造最適化方法は原理的に正方晶などの最安定構造を正しく評価し,正確なエネルギーゲインを与える.
- 本最適化方法によりはじめて数値的に全エネルギーをuの関数として表すことができた.
- 全エネルギー,格子定数cとa,変位の「方向」をuの関数として全自動的に評価できる.
である.
本最適化方法はBaTiO3とPbTiO3の性質の違いをより明らかにしただけではなく,
強誘電体の分子動力学シミュレーションのための有効ハミルトニアンの各パラメーターを決定するためにも有用である
[Takeshi Nishimatsu et al.: Phys. Rev. B 82, 134106 (2010), doi:10.1103/PhysRevB.82.134106].
本方法の応用例
本手法はABO3型の強誘電体だけではなく,RushchanskiiらによってSn2P2S6という特異な強誘電体の解析にも応用されている
[Konstantin Z. Rushchanskii, Yulian M. Vysochanskii and Dieter Strauch: Phys. Rev. Lett. 99, 207601 (2007), doi:10.1103/PhysRevLett.99.207601].
独自コードによる強誘電体薄膜キャパシタのヒステリシス・ループの超高速分子動力学シミュレーション
本研究の背景
強誘電体薄膜キャパシタは不揮発性ランダムアクセスメモリ (FeRAM)
などに幅広く応用され,
その微細化(ダウンサイジング)が強く求められているところである.
一方,強誘電体キャパシタの特性は
強誘電体と電極との間の界面の状態に大きく影響を受けるということがよく知られている.
例えば,
強誘電体キャパシタの疲労は,
電極近くの不活性層が原因となっている.
また,電極による遮蔽が不完全な場合には,
強誘電体薄膜中に反分極場が部分的に残ってしまい,
膜厚が薄くなるにしたがって
抗電場 (coercive electric field) Ecが小くなるであろうということが予想されている.
しかしながら,強誘電体キャパシタの誘電緩和,ヒステリシス・ループ,分極反転,ドメイン壁の動力学的研究は,
それらの温度依存性やナノサイズ効果の理解もふくめて困難であった.
その理由は,実験的には「その場観察」が難しく,
理論的には長距離の双極子−双極子相互作用が大規模・長時間の分子動力学シミュレーションを不可能にしていたためである.
今までは,また,強誘電体−電極間界面構造によって引き起こされる表面効果や反分極場をどのようにシミュレーションに取り込むかが明確ではなかった.
計算手法と高速化手法
西松は上述の問題を解決した分子動力学シミュレーションコードferamを開発した.
http://loto.sourceforge.net/feram/ に於いてフリーソフトウエアとして公開している.
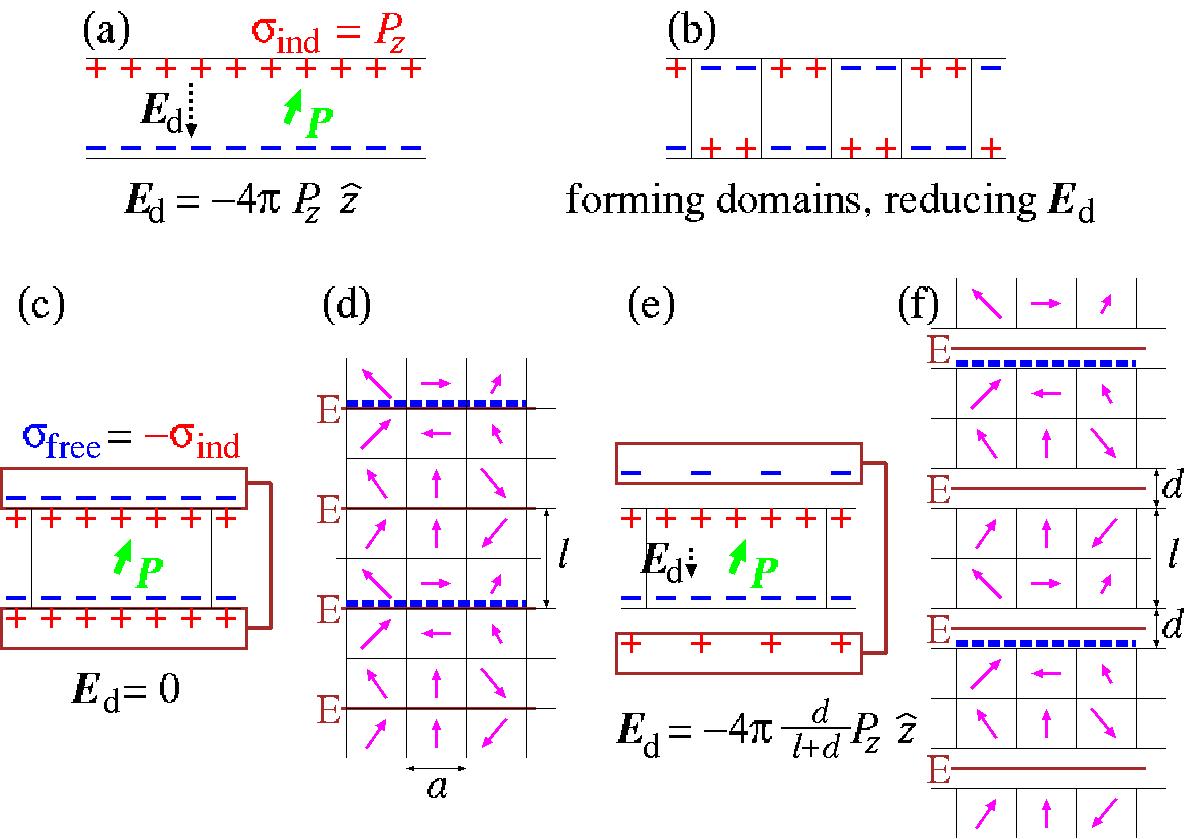
feramコードは,周期的境界条件(図3)の下,
ペロプスカイト型強誘電体ABO3の第一原理計算で求められた有効ハミルトニアンHeff
に基づいた分子動力学計算を行う.
従前のモンテカルロ法と違い,分子動力学計算は真の時間発展計算が可能である.
長距離の双極子−双極子相互作用と非一様歪みは,そのk-局所性 (k-locality) を用いて逆空間で計算され,
その他のr-局所的な項は実空間で計算される.
実空間と逆空間との間の変換は高速フーリエ変換 (FFT) を使うため,
今まではN2に比例(O(N2),ここでNはスーパーセル中のユニットセルの数)
していた双極子−双極子相互作用の計算時間が大幅に短縮されO(NlogN)となっている.
また,OepnMPによって並列化されている.
その結果,強誘電体薄膜キャパシタの実際的な規模(システムサイズ,〜100 nm)と時間(〜1 ns)でのシミュレーションが可能となった.
現在までferamコードは強誘電体薄膜キャパシタの分極特性の温度特性の研究
[Jaita Paul, Takeshi Nishimatsu et al.: Phys. Rev. Lett. 99, 077601 (2007), doi:10.1103/PhysRevLett.99.077601] や
疲労によりダメージを受けたキャパシタのヒステリシス・ループの再現
[Takeshi Nishimatsu et al.: Phys. Rev. B 78, 104104 (2008), doi:10.1103/PhysRevB.78.104104] などに成功している.
特に後者の論文は論文誌のEditors' Suggestionに選ばれ,また,論文中の図が2008年9月のPRB Kaleidoscope Imagesのひとつにも選ばれるなど高い評価を得ている.
feramコードの将来性
本feramコードは現在その応用がますます広がりつつある強誘電体の物性の解析と理解のための強力なツールとなりうる.
半導体中の不純物の第一原理計算による研究
ダイヤモンド中のドナー−水素複合欠陥の第一原理計算
ダイヤモンド中の孤立置換型ドナー不純物であるリン(P),硫黄(S),いくつかのサイトに置かれた孤立水素(H),
そしてドナー不純物と水素から構成される不純物複合体 (PH-,SH-不純物複合体) の3種類の点欠陥について,
局所密度近似にもとづいた第一原理計算を行ないその電子状態と安定な原子配置を決定した.
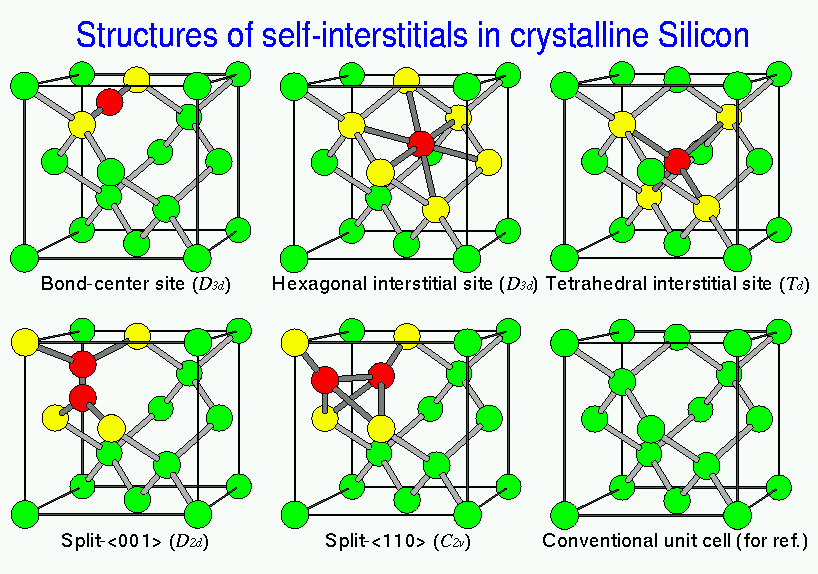
P,SともJahn-Teller効果によってその不純物周りの対称性が落ちることがわかった.
H不純物については,ボンド間サイトがtetrahedralサイトやhexagonalサイト,
anti-bondingサイトに比べて安定な位置であることがわかった.
この結果はmuon-spin-rotation(μSR)の実験結果と一致する.
われわれはまた,H不純物はPドナーを不活性化することを確認した.
SH-不純物複合体についてはその化学結合の様相を明らかにし,
Sダブルドナーの不純物準位が伝導帯の底から1.63 eVであるのに対して,
SH-不純物複合体のそれは1.07 eVとより浅くなることを予想した.
ドナー水素不純物複合体についてはその赤外活性周波数を予測した.
また,低抵抗n型ダイヤモンド半導体の実現のためのドーピング方法を提案た.
["ab initio Study of Donor-Hydrogen Complexes for Low-Resistivity n-Type Diamond Semiconductor",
Takeshi Nishimatsu,Hiroshi Katayama-Yoshida, Nozomi Orita, Jpn. J. Appl. Phys., Vol.41, pp.1952-1962 (2002)]
シリコン中の自己格子間原子の第一原理計算